CONCEITUAÇÃO
Um escoamento uniforme é um movimento permanente no qual a velocidade é constante ao longo de cada trajetória.
A trajetória de uma partícula é o lugar geométrico dos pontos ocupados pela partícula ao longo do tempo.
Num escoamento permanente, também chamado de estacionário, a velocidade é função das coordenadas, mas independente do instante considerado, isto é, a velocidade varia de ponto para ponto, mas mantém-se constante ao longo do tempo.
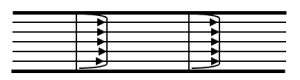
Num escoamento uniforme, as trajetórias, além de retilíneas, são paralelas:

De acordo com o teorema de Bernoulli, um líquido perfeito em movimento permanente tem a energia mecânica total (H) (por unidade de peso do líquido) constante ao longo da trajetória.

Sendo \(H=\frac{p}{\gamma}+z+\frac{V^{2}}{2g}\), onde
p é a pressão num dado ponto,
z é a cota geométrica desse ponto,
V é a velocidade de uma partícula do líquido no ponto,
\({\gamma}\) é o peso específico do líquido e
g é a aceleração da gravidade
O termo \(\frac{p}{\gamma}\) é chamado de potencial de pressão e o termo \(\frac{V^{2}}{2g}\) é chamado de altura cinética.
A soma \(\frac{p}{\gamma}+z\) é chamada de cota (ou carga) piezométrica.
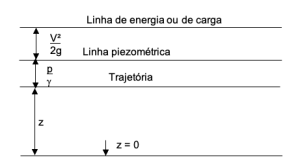
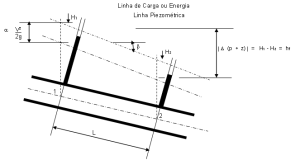
Considerando a trajetória de uma partícula do líquido, se nós plotarmos, a partir das  cotas geométricas  z os  valores de  \(\frac{p}{\gamma}\)  nós obtemos uma linha chamada de linha piezométrica e a partir dessa linha, se nós adicionarmos os valores  V²/2g nós teremos a linha de energia (por unidade de peso do líquido):

No caso de fluidos reais em movimento, a energia total H diminui ao longo da trajetória:

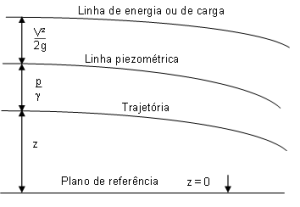
A variação da cota da linha de energia entre dois pontos ( 1 e 2 ) da trajetória da partícula de um líquido real é denominada perda de carga ( hf ):

Assim \(H_{1}-H_{2} = H_{f}\) ou \(\frac{p_{1}}{\gamma}+z_{1}+\frac{V_{1}^{2}}{2g}=\frac{p_{2}}{\gamma}+z_{2}+\frac{V_{2}^{2}}{2g}\)

A perda de carga por unidade de comprimento da trajetória é denominada Sf; (Grandeza adimensional) e é conhecida como perda de carga unitária:
\(h_{f}=S_{f}\)
\({\Delta}L\)
onde \({\Delta}L\) é a distância medida ao longo da linha de centro de gravidade das seções.
Considere agora um tubo de fluxo cujo movimento é uniforme: em uma dada seção, a cota piezométrica é comum para todos os pontos da seção. Um perfil típico de variação de velocidades ao longo de uma seção transversal de um tubo de 100 mm de diâmetro para variados valores de vazão é mostrado a seguir:

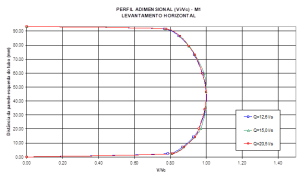
Como a velocidade não é igual nas diferentes trajetórias, a cada trajetória corresponde uma linha de energia diferente:

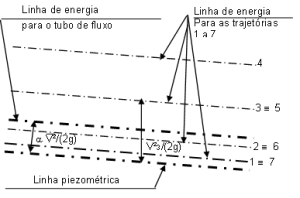
É necessário se definir uma linha de energia correspondente ao escoamento na totalidade da seção.
A energia ou carga referida a toda a seção é dada por:
\(H=\frac{p}{\gamma}+z+\alpha\frac{V^{2}}{2g}\)
Onde \(V\) é a velocidade média na seção: \(V=\frac{Q}{A}\)
onde Q é a vazão que passa pela seção e A é a área da seção.
\(\alpha=\frac{\int A V^3 dA}{V^3 A }\) é conhecido como coeficiente de Coriolis.

O teorema de Bernoulli pode então ser expresso como:

\(d \cdot \frac{\frac{p}{\gamma}+z+\frac{V^{2}}{2g}}{dL}=-S_{f}\)

Em um escoamento sob regime uniforme, a perda de carga unitária Sf é constante e a linha de energia retílinea.
A linha piezométrica é paralela à linha de energia porque \(\alpha \cdot V^2\) é constante ao longo do percurso. A perda de carga unitária pode assim ser determinada pelo quociente entre a diminuição da cota piezométrica entre duas seções transversais e a distância L entre as mesmas:

\(Sf= \frac{\Delta \left | \frac{p}{\gamma}+Z \right |}{L}\)

Numa seção com velocidade uniforme \(\alpha =1\). Quanto mais uniforme for a distribuição de velocidades, mais próximo da unidade será \(\alpha\).

A partir deste ponto, para nossas aplicações, nós vamos admitir que \(V =\overline{V}\) e \(\alpha =1\).

 

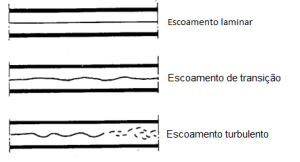
ESCOAMENTOS LAMINAR E TURBULAMENTO
Experiência de Reynolds:

 

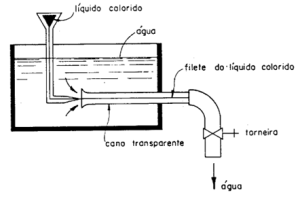
Deixando a água escorrer pelo cano transparente juntamente com o líquido colorido, forma-se um filete desse líquido. O escoamento da água está em regime laminar.
Aumentando a vazão da água abrindo-se a torneira, nota-se que o filete vai se alterando podendo chegar a difundir-se na massa líquida. Nesse caso o escoamento da água ocorre em regime turbulento .

 

Para se determinar o tipo de escoamento em uma canalização, calcula-se o número de Reynolds dado pela expressão.

\(Re = \frac{V \cdot D}{\nu}\)

onde:
Re= número de Reynolds (adimensional)
V = velocidade (\(m/seg\))
D = diâmetro do conduto (m)
\(\nu\) = viscosidade cinemática (\(m^2/seg\))

Para os tubos comerciais valem aproximadamente os seguintes limites:

Re < 2.000 : Escoamento Laminar

Nas condições práticas, o escoamento da água em canalizações é sempre turbulento.

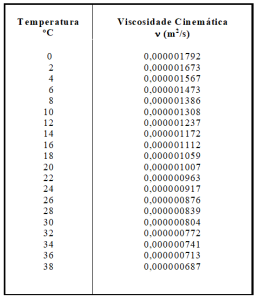
A viscosidade cinemática da água varia com a temperatura de acordo com os valores quadro 1.

 

FÓRMULA DA DARCY-WEISBACH PARA PERDA DE CARGA EM TUBULAÇÕES

\(hf=f\frac{L}{D}\frac{V^2}{2g}\)

onde f é o chamado fator de atrito.

Os resultados das experiências de Nikarudse em tubos circulares de diâmetro D, com diferentes rugosidades (rugosidades artificiais criadas por grãos de areia de diâmetro), conclui-se que a resistência ao escoamento era a mesma para todos os tubos (lisos ou rugosos) até determinados valores do número de Reynolds:

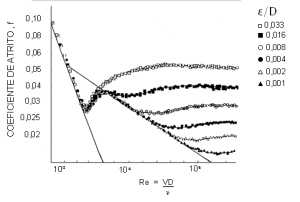
Quando o número de Reynolds é maior que determinados limites, então a resistência ao escoamento é condicionada unicamente pela turbulência, ou:

\(f = \phi_{2}\cdot \frac{\varepsilon }{D}\), onde \(\frac{\varepsilon }{D}\) é a chamada rugosidade relativa.

Nesse caso, o regime é denominado turbulento rugoso ou simplesmente turbulento.

Para esta região, Karman e Prandtl propuseram:

\(\frac{1}{\sqrt{f}}=2log\cdot \frac{3,7D}{\varepsilon }\)

Colebrook propôs uma lei única para tubos comerciais, válida em todo o domínio dos escoamentos turbulentos:

\(\frac{1}{\sqrt{f}}=- 2log\cdot \frac{\varepsilon}{3,7D }+\frac{2,51}{Re\cdot \sqrt{f}}\)

Conhecida como fórmula de Colebrook – White.
Observe que nessa fórmula nós não podemos obter f separadamente em um lado da equação, portanto, teremos que iterativamente achar f. A rugosidade absoluta equivalente \(\varepsilon\) pode ser obtida em função do material da tubulação, de acordo com quadro 2.

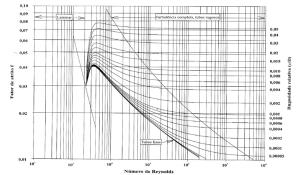
A equação de Colebrook – White está representada graficamente pelo diagrama de Moody, apresentado a seguir, o qual apresenta eixos coordenados com graduação logarítimica, com valores de f como ordenada e Re como abcissa. Nesse diagrama, figuram curvas f = (Re) para determinados valores da rugosidade relativa.

Infelizmente a solução da equação de Colebrook – White (o coeficiente de atrito f) só pode ser obtida iterativamente, pois f aparece em ambos os lados da equação. Swamee e Jain1 desenvolveram uma fórmula explícita para f.

\(f = \frac{0,25}{\left (log\left ( \frac{\varepsilon }{3,7D} + \frac{5,74}{Re^{0,98}} \right )\right )^2}\)

Tal fórmula apresenta um erro de 2% em relação a fórmula de Colebrook – White para 10־⁵ < Ɛ < 2 x 10ֿ־² e 4 x 10³ < Re < 10⁸.

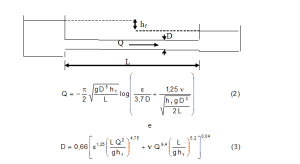
Tal magnitude de erro é perfeitamente aceitável visto que o erro inerente na determinação da rugosidade pode chegar a 10%. Swamee e Jain também desenvolveram fórmulas explícitas para determinação dea vazão Q e do diâmetro D para o caso de um escoamento entre dois reservatórios, conforme a figura:

Referências
SWAMEE, P.K. e JAIN, A. K. Explicit Equations for pipe-flow problems, Journal of the Hydraulics Division – ASCE, v. 102, n.NY5, p. 657-664, 1976.