FÓRMULAS EMPÍRICAS PARA O CÁLCULO DA PERDA DE CARGA

Origem

De um modo geral as fórmulas empíricas têm sua origem a partir de experiências, sob certas condições e limitadas por condições específicas. O pesquisador analisa os resultados encontrados e conclui por uma expressão que relaciona os valores medidos. Por não terem origem em fundamentos analíticos, seus resultados são limitados e só devem ser utilizadas em condições que se assimilem as de sua origem. Para cálculo de sistemas de abastecimento de água em escoamento são freqüentemente empregadas as expressões de Hazen-Williams (1902) para escoamentos sob pressão e de Chézy (1775) para escoamentos livres.

Fórmula de Hazen-Williams (1902)

Desenvolvida pelo Engenheiro Civil e Sanitarista Allen Hazen e pelo Professor de Hidráulica Garden Williams, entre 1902 e 1905, é, sem dúvida, a fórmula prática mais empregada pelos calculistas para condutos sob pressão, desde 1920. Com resultados bastante razoáveis para diâmetros de 50 a 3000mm, com velocidades de escoamento inferiores a 3,0 m/s, é equacionada da seguinte forma:

Onde:
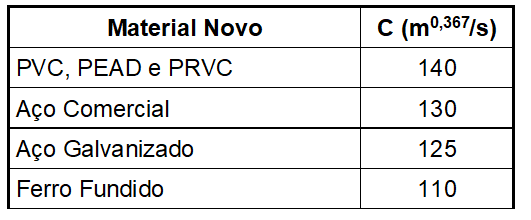
C – coeficiente de rugosidade que depende do material (tabelado), em \(m^{0,367}/s\)
D – diâmetro, em m
Q – vazão, em \(m^{3}/s\)
L – comprimento, em m

Esta expressão tem como limitação teórica o fato de assumir o escoamento como sempre completamente turbulento e desconsiderar a influência da temperatura.

Tabela de Coeficiente C de Hazen-Willians

Perdas de carga localizadas

onde K_L é o coeficiente de perda de carga localizada o qual depende principalmente da geometria do componente. Perda de carga localizada devido ao alargamento brusco da seção:

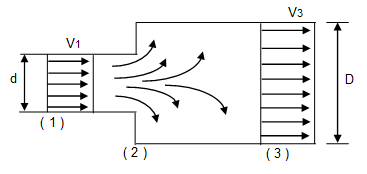
Considerar um volume de controle nós podemos entre as seções (1) e (3) e usar a equação da continuidade \(A_{1}\cdot V_{1}=A_{2}\cdot V_{2}\)

Considerando a pressão na seção (2) (p₂) igual a p1, nós podemos utilizar a equação do momento entre as seções (2) e (3), resultando em:

\(p_{1}\cdot A_{3}-p_{3}\cdot A_{3}=\rho \cdot A_{3}\cdot V_{3}\cdot \left ( V_{3}-V_{1} \right )\) finalmente nós podemos usar a equação de Bernoulli entre as seções (1) e (3) teremos:

\(\frac{p_{1}}{\gamma }+\frac{V_{1}^{2}}{2g}=\frac{p_{3}}{\gamma }+\frac{V_{3}^{2}}{2g}+h_{L}\)

Considerando \(h_{L}=K_{L}\cdot \frac{V_{1}^{2}}{2g}\)

nós podemos chegar combinando as equações acima:

\(K_{L}=1-\frac{A_{1}}{A_{2}}\)

se plotarmos essa equação teremos: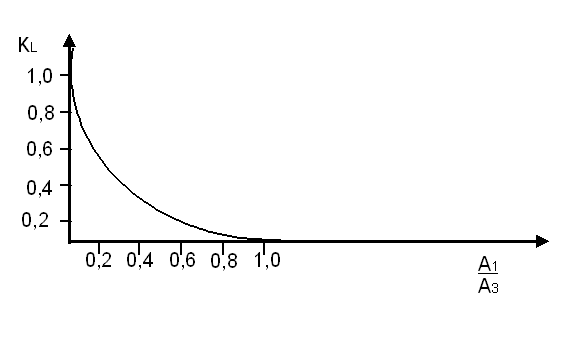

O que está de acordo com resultados experimentais, é interessante notar que o caso de uma canalização conectada a um tanque:

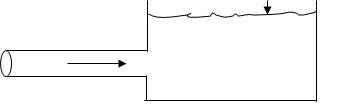
Corresponde ao caso de expansão no qual a velocidade V3 ≅ 0 se nós remanejarmos a equação (1), com \(A_{1}=\frac{A_{3}\cdot V_{3}}{V_{1}}\) obteremos \(K_{L}=1-\frac{V^{2}_{3}}{V_{1}}=\frac{V_{1}-V_{2}}{V_{1}}\) portanto, como \(V_{3}\cong 0 \Rightarrow K_{L}=1\).

As Tabelas a seguir contém valores de K_L para diversos valores de D/d. Importante: a velocidade que se usa para o cálculo nesse caso é V₁. (A maior velocidade):

Tabela 3.a) Valores de K_L para redução brusca de seção

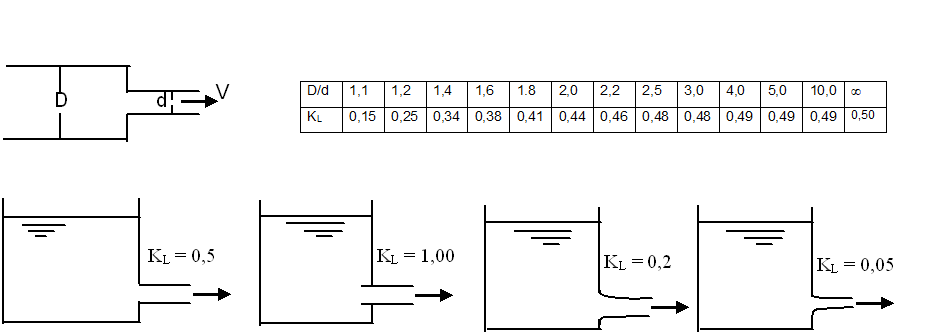
Tabela 3.b) Valores de K_L para aumento brusco de seção

Perdas de carga localizada devido a um alargamento gradual da seção

A perda de carga pode ser grandemente reduzida com a introdução de uma transição gradual, como mostra a figura abaixo:

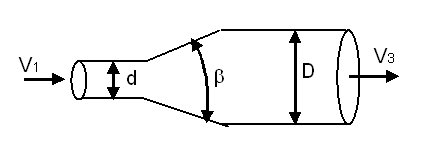
O ângulo \(\beta > 35^{\circ }\) a expansão gradual é menos eficiente que a expansão brusca (\(\beta = 180^{\circ }\)) e que existe uma ângulo ótimo ( em torno de \(8^{\circ }\) ), para o qual a perda de carga é mínima.

Perdas de carga localizada devido a um estreitamento brusco da seção

Como no caso de um alargamento brusco, para um estreitamento brusco da seção da canalização:

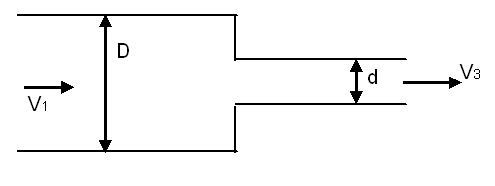
O coeficiente de perda de carga localizada K_L depende dos diâmetros D e d.

A tabela 3.a contém valores de K_L em função de valores do quociente D/d: usada neste caso é importante: a velocidade observe que o caso D = \infty corresponde ao caso da saída de água de um reservatório para um conduto:

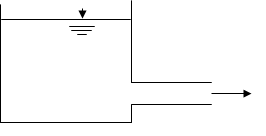
É denominada saída normal aquela em que o conduto faz um ângulo, de 90º com as paredes do reservatório ( ver figura acima) neste caso, KL = 0,5, para outros tipos de saída, consultar tabela 3.a.

Tabela 4.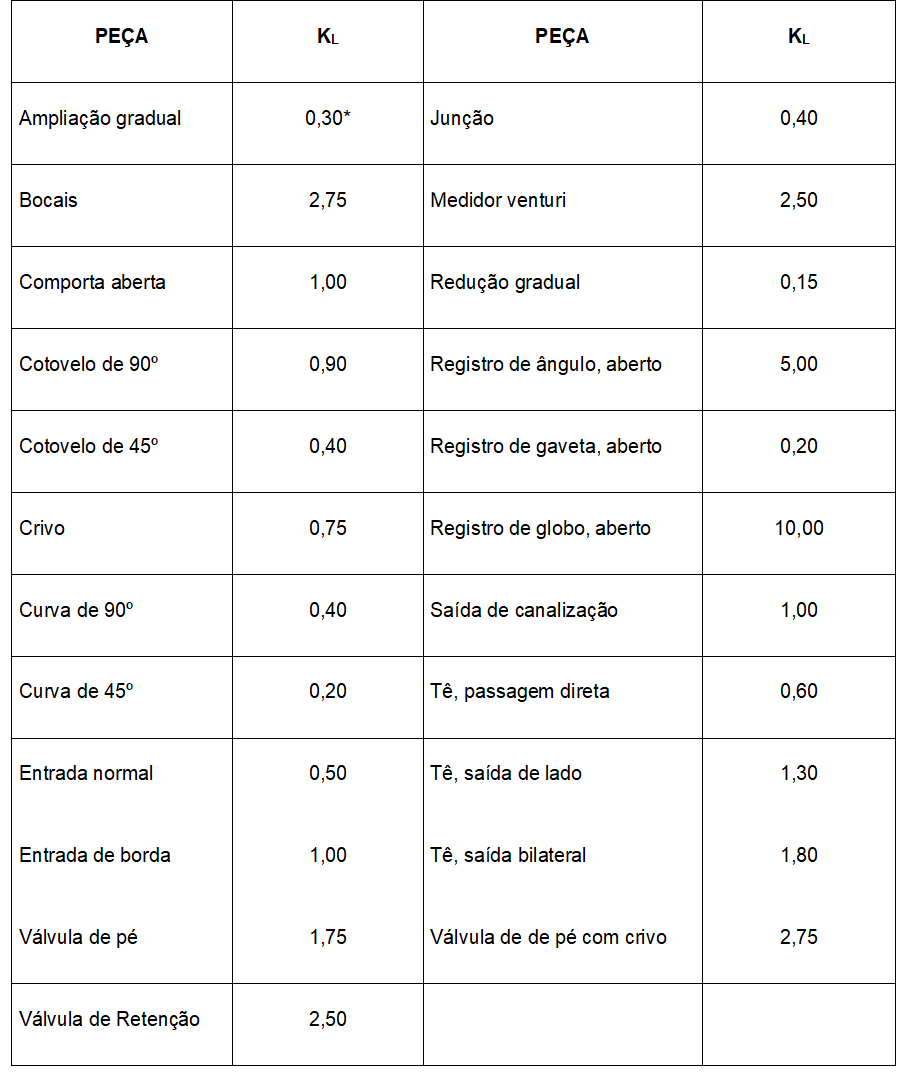

Exemplos de peças que causam perda de Carga Localizada

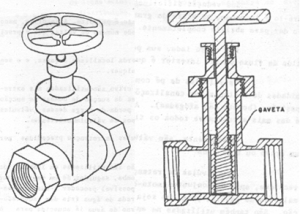
Figura 1.1. Registro ou Válvula de Gaveta

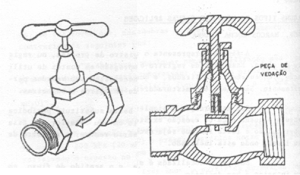
Figura 1.2. Registro ou Válvula de Pressão ou Globo

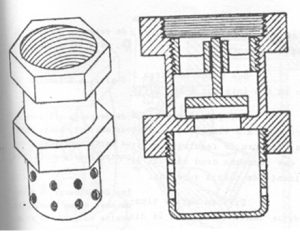
Figura 1.3. Válvula de Pé com crivo

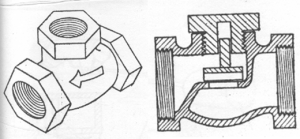
Figura 1.4. Válvula de Retenção

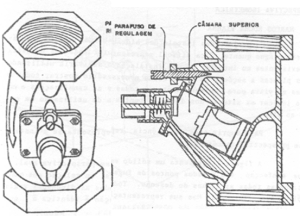
Figura 1.5. Válvula de Descarga