ESCOAMENTO EM TUBOS PARALELOS

Considere o seguinte trecho de um sistema de distribuição:

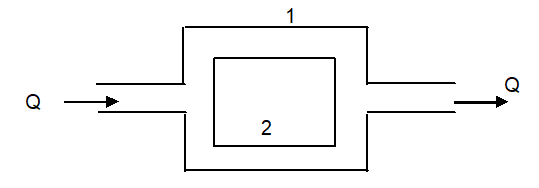
Em geral, nós vimos que \(hf = K\cdot Q^{2}\).

Designando \(hf^{_{1}}\) a perda de carga no trecho 1 e \(hf^{_{2}}\) a perda no trecho 2, teremos:

\(hf_{1}=K_{1}\cdot Q^{2}_{1}\)                                 (A)
\(hf_{2}=K_{1}\cdot Q^{2}_{2}\)

mas \(hf_{1}=hf_{2} \rightarrow K_{1}\cdot Q^{2}_{1}=K_{2}\cdot Q^{2}_{2}\)

\(Q_{2}=\left ( \frac{K_{1}}{K_{2}} \right )^{0,5}\cdot Q_{1} \)                         (B)

Sabemos também que:

\(Q=Q_{1}+Q_{2}\)                                     (C)

Através de (B) e (C) nós podemos achar \(Q_{1}\), \(Q_{2}\) e \(hf\).

Exemplo 1

\(K_{1}=4029\frac{s^{2}}{m^{5}}\) e \(K_{2}=23264\frac{s^{2}}{m^{5}}\)

\(Q=0,142\frac{m^{3}}{s}\)

De (C) \(\rightarrow Q_{2}=0,142\cdot Q_{1}\)

De (B) \(\rightarrow 0,142\cdot Q_{1} = 0,146\cdot Q_{1} \rightarrow Q_{1}=0,100\frac{m^{3}}{s}\)

De (C) \(Q_{2}=0,042\frac{m^{3}}{s}\)

e de (A) \(\rightarrow hf=40 m\)

PROBLEMAS DOS TRÊS RESERVATÓRIOS

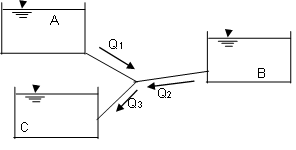
Considere o seguinte sistema de reservatórios e tubos:

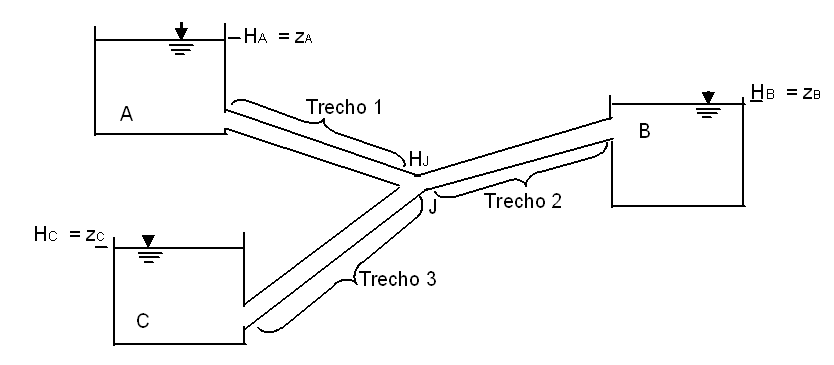
Onde\(H_{J}\) é a energia ou carga total no nó de junção J.

No sistema acima, pode haver três possibilidades:

Caso 1: \(H_{J} > H_{B}\), nesse caso, \(Q_{1}=Q_{2}+Q_{3}\)

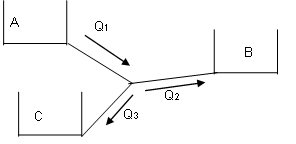
Caso 2: \(H_{J} = H_{B}\), nesse caso, \(Q_{1}=Q_{3}\) e \(Q_{2}=0\)

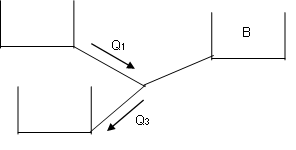
Caso 3: \(H_{J} < H_{B}\), nesse caso, \(Q_{3}=Q_{1}+Q_{2}\)

Vamos estudar agora caso a caso:

Caso 1: aplicando a equação da energia para o escoamento entre A e C.

\(H_{A}=H_{C}+ hf\)
\(H_{A}=H_{C}+hf_{1} + hf_{3}\) ou
\(H_{A}-hf_{1}= H_{C} + hf_{3}\rightarrow Z_{A}-K_{1}\cdot Q^{2}_{1} = Z_{C}-K_{3}\cdot Q^{2}_{3}\)

E entre A e B

\(H_{A}-hf_{1}= H_{B} + hf_{2}\rightarrow Z_{A}-K_{1}\cdot Q^{2}_{1} = Z_{C}-K_{2}\cdot Q^{2}_{2}\)

 

Por continuidade, nós sabemos que:

\(Q_{1}=Q_{3}+Q_{2}\)            (três equações, três incógnitas)

Caso 2 – de maneira similar:

\(Z_{A}-K_{1}\cdot Q^{2}_{1}=Z_{C} +K_{3}\cdot Q^{2}_{3}\)

\(Q_{1}=Q_{3}\)                   (duas equações, duas incógnitas)

Caso 3

\(Z_{A}-K_{1}\cdot Q^{2}_{1}=Z_{C} +K_{3}\cdot Q^{2}_{3}\)
\(Z_{B}-K_{2}\cdot Q^{2}_{2}=Z_{C} +K_{3}\cdot Q^{2}_{3}\)         e
\(Q_{3}=Q_{1}+Q_{2}\)

Normalmente nós assumimos que temos caso 2 e calculamos Q₁ e Q₃ se Q₁ < Q₃, a continuidade não está satisfeita e se trata do caso 3, se Q₁ > Q₃ também a continuidade não está satisfeita e se trata do caso 1.

Exemplo 2

Considere o seguinte problema de três reservatórios:

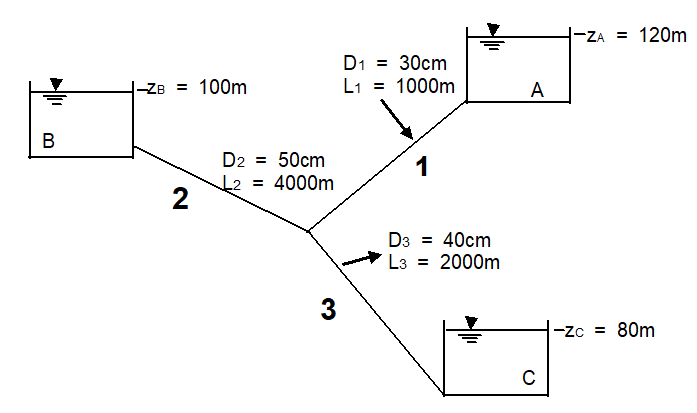
Se os tubos são feitos de concreto com \(\varepsilon =0.60 mm\) e a temperatura é de 20ºC, calcule a vazão em cada tubo:

Vamos inicialmente considerar que ocorre em todos os tubos o regime completamente turbulento, (essa hipotése terá de ser verificada no final), nós podemos usar a fórmula de Karman & Prandtl.

\(\frac{1}{\sqrt{f}}=2log\cdot \frac{3.7D}{\varepsilon }\)

 

com \(\varepsilon =0.60 mm\)

Assim:
Trecho 1 – \(D_{1}=300mm \rightarrow f_{1}=0,023\)
Trecho 2 – \(D_{2}=500mm \rightarrow f_{2}=0,021\)
Trecho 3 – \(D_{3}=400mm \rightarrow f_{3}=0,022\)

Dessa forma:

\(K_{1}=\frac{f_{1} L_{1}}{2gD_{1}A^{2}_{1}}=\frac{8f_{1}L_{1}}{\pi ^{2}gD_{1}^{5}}=782\frac{s^{2}}{m^{5}}\)
\(K_{2}=222\frac{s^{2}}{m^{5}}\)
\(K_{3}=355\frac{s^{2}}{m^{5}}\)

 

Como vimos, vamos inicialmente assumir o caso 2:

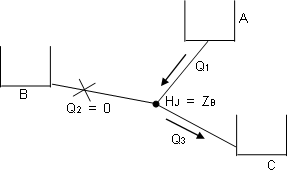
Nesse caso:

\(hf_{1}=120-100=20m\)
\(Q_{1}=\left ( \frac{hf_{1}}{K_{1}} \right )^{0,5}=0,160\frac{m^{3}}{s}\)
\(hf_{3}=100-80=20m\)
\(Q_{3}=\left ( \frac{hf_{3}}{K_{3}} \right )^{0,5}=0,237\frac{m^{3}}{s}\)

Como \(Q_{3}>Q_{1}\rightarrow\) caso 3

\(Z_{A}-K_{1}\cdot Q^{2}_{1}=Z_{C}+K_{3}\cdot Q^{2}_{3}\)

\(Z_{B}-K_{2}\cdot Q^{2}_{2}=Z_{C}+K_{3}\cdot Q^{2}_{3}\) ou

\(Q_{1}=\left ( 0,0512-0,454\cdot Q^{2}_{3} \right )^{0,5}\) \(Q_{2}=\left ( 0,0901-1,599\cdot Q^{2}_{3} \right )^{0,5}\)

 

Usando ainda \(Q_{3}=Q_{1}+Q_{2}\) teremos:

\(Q_{1}=0,164\frac{m^{3}}{s}\)
\(Q_{2}=0,067\frac{m^{3}}{s}\)
\(Q_{3}=0,231\frac{m^{3}}{s}\)

Verificação do coeficiente de atrito usado:

Trecho 1 – \(V_{1}=\frac{Q_{1}}{A_{1}}=2,32\frac{m}{s}\)

\(Re = 696038\)

 

Assim:

\(f_{1}=\frac{0,25}{\left ( log\cdot \left ( \frac{\varepsilon }{3,7D}+\frac{5,74}{Re^{0,9}} \right ) \right )^{2} } = 0,024\)

 

Trecho 2 – \(V_{2}=\frac{Q_{2}}{A_{2}}=0,341\frac{m}{s}\)

\(Re = 170614\) \(f_{2}=0,025\)

 

Trecho 3 – \(V_{3}=\frac{Q_{3}}{A_{3}}=1,84\frac{m}{s}\)

\(Re = 735296\) \(f_{2}=0,024\)

 

EXERCÍCIOS PROPOSTOS

Exercício 1

Dado o seguinte sistema, com dois tubos paralelos:

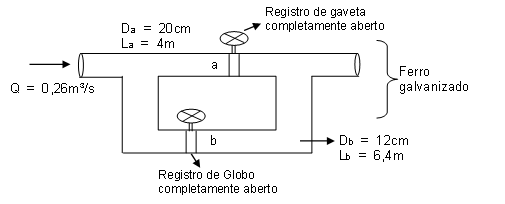
Levando em consideração as perdas localizadas e sabendo que a temperatura é de 10º C, determine a vazão em cada um dos tubos.

Solução

\(A_{a}=0,0314m^{2}\)
\(A_{b}=0,0113m^{2}\)

por continuidade

\(0,26 = A_{a}\cdot V_{a} + A_{b}\cdot V_{b}\)
\(0,26 = 0,0314\cdot V_{a} + 0,0113\cdot V_{b}\)
\(h_{a}=f_{a}\cdot \frac{L_{a}}{D_{a}}\cdot \frac{V_{a}^{2}}{2g}+\sum K_{L}\cdot \frac{V_{a}^{2}}{2g}\)

Considerando o regime completamente turbulento:

\(f_{a}=0,018\)
\(\sum K_{L} = K_{L}\left ( T \right ) + K_{L}\left ( Registro de gaveta \right )\)

Portanto \(h_{a}=0,0591\cdot V^{2}_{a}\)

\(h_{b}=\frac{f_{b}\cdot L_{b}}{D_{b}}\cdot \frac{V^{2}_{b}}{2g}+\sum K_{L}\cdot \frac{V^{2}_{b}}{2g}\)
\(f_{b}=0,021\)

e

\(\sum K_{L} = K_{L} \left ( T saida lado \right )+2K_{L}\left ( Cotovelo90 \right )+K_{L}(registroGlobo)=14,4\)

 

Portanto \(h_{b}=0,791V_{b}^{2}\)

Como \(h_{a}= h_{b}\)

\(V_{a}= 3,66 V_{b}\)

 

Usando a equação da continuidade:

\(V_{b}=2,06\frac{m}{s} e V_{a}=7,54\frac{m}{s}\)

 

Verificando o coeficiente de atrito:

Ramo a: \(\nu = 1,31\times 10^{-6}\frac{m}{s}\) para T = 10ºC.

\(Re=1128244\)

 

Assim \(f_{a}=0,019\) o que pode ser considerado aceitável para o ramo b:

\(Re=228092\)
\(f_{a}=0,019\) o que também é aceitável.

Exercício 2

Dado o seguinte sistema de tubos e reservatórios:

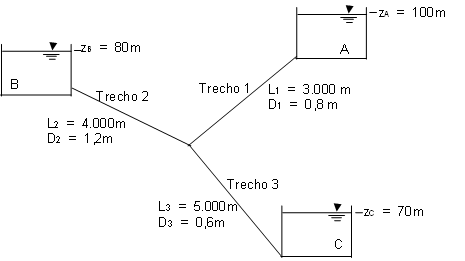
Sabendo que \(\varepsilon = 0,05mm\) e que a temperatura da água é de 20ºC, calcule a vazão em cada um dos trechos:

Solução

Considerando inicialmente regime completamente turbulento em todos os tubos.

Trecho 1: \(f_{1}=0,011\)
Trecho 2: \(f_{2}=0,010\)
Trecho 3: \(f_{3}=0,012\)

Assim

\(K_{1}=8,321\frac{s^{2}}{m^{5}}\)
\(K_{2}=1,328\frac{s^{2}}{m^{5}}\)
\(K_{3}=63,760\frac{s^{2}}{m^{5}}\)

Vamos assumir inicialmente o caso 2:

\(Q_{1}=\left ( \frac{20}{8,321} \right )^{0,5}=1,55\frac{m^{3}}{s}\)
\(Q_{3}=\left ( \frac{10}{63,76} \right )^{0,5}=0,396\frac{m^{3}}{s}\)

Como \(Q_{3}< Q_{1}\rightarrow\) caso 1.

\(Z_{A}-K_{1}\cdot Q^{2}_{1}=Z_{C}+K_{3}\cdot Q^{2}_{3}\)
\(Z_{A}-K_{1}\cdot Q^{2}_{1}=Z_{B}+K_{2}\cdot Q^{2}_{2}\)

\(Q_{3}=\left ( 0,471-0,131 \cdot Q^{2}_{1} \right )^{0,5}\)
\(Q_{3}=\left ( 15,06-6,266 \cdot Q^{2}_{1} \right )^{0,5}\)

Usando ainda \(Q_{1}=Q_{2}+Q_{3}\)

Teremos

\(Q_{1}= \left ( 0,471-0,131 \cdot Q^{2}_{1} \right )^{0,5} + \left ( 15,06-6,266 \cdot Q^{2}_{1} \right )^{0,5}\)

 

Resolvendo iterativamente a equação acima teremos:

\(Q_{1}= 1,49\frac{m^{3}}{s}\)
\(Q_{2}= 1,07\frac{m^{3}}{s}\)
\(Q_{3}= 0,42\frac{m^{3}}{s}\)

Verificação do coeficiente de atrito:

\(V_{1}=\frac{Q_{1}}{A_{1}}=2,96\frac{m}{s}\)
\(f_{1}=0,012\)
\(f_{2}=0,012\)
\(f_{3}=0,013\)