1. Introdução

Uma tubulação, funcionando como um condutor forçado, destinada a conduzir água entre as unidades de um sistema de abastecimento ou de uma rede de irrigação está sujeita a alterações abruptas em relação ao seu estado permanente. Estas alterações nas vazões ou nas pressões, causam o fenômeno dos transientes hidráulicos ou Golpe de Ariete.  Estas mudanças bruscas podem ter várias causas:

• Abertura ou fechamento abrupto de válvulas, registros, comportas ou Sifões.
• Partidas e paradas “normais” de bombas.
• Parada Abrupta de bombas (Falta de energia).
• Enchimento/Esvaziamento de Adutoras que efetivamente não pode ser prevenida

A terceira causa está em negrito pois é a única que, previamente, não pode ser prevenida ou evitada com medidas e dispositivos de atenuação como fechamento lento dos registros, No-Breaks, Inversores de frequência ou Ventosas.

Devido a essas mudanças, altas e baixas pressões são formadas, surgindo uma onda com velocidade próxima da velocidade do som no líquido. Com a intensidade da onda, equipamentos sofrem sérios riscos de ficarem danificados ou até mesmo de entrarem em colapso, ocasionando perdas materiais ou até perdas humanas. Visto que, compreende-se a importância do estudo do fluxo num regime transiente, demandando mais difusão nos cursos de Engenharia e Agronomia (BARBOSA et al., 2018).

Durante o período transitório, ocorrem variações de pressão e vazão em um curto ou longo espaço de tempo, podendo provocar o chamado de golpe de aríete, cujo sinônimo é fluxo instável do qual o nome originou-se após um som característico que ocorreu durante uma pancada de um martelo. Para melhor compreensão do transiente hidráulico, efeitos colaterais devem ser considerados, tais como cavitação transitória e separação de coluna (ADAMKOWSKI & LEWANDOWSKY, 2009).

2. Equação de Allievi-Joukowsky

A descrição da sequência de eventos do golpe de aríete pode ser feita utilizando um exemplo simples onde ocorre o fechamento repentino de uma válvula localizada na extremidade de um conduto, de comprimento \(L\), que sai de um reservatório, conforme pode ser visualizado na Figura 1:

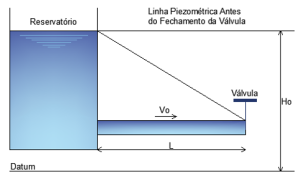
Figura 1 – Reservatório com conduto e válvula a jusante

O fluído escoa com uma velocidade constate \(V_{0}\), densidade \({\rho}_{0}\) e pressão inicial à montante da válvula de \(p_{0}\). Além disso, o escoamento se processa somente pela gravidade, despreza-se o atrito e considera-se que o sistema deve ser assentado no plano horizontal e que a tubulação e a água formam um sistema perfeitamente elástico.

Fechando-se a válvula no instante \(t = 0\), a velocidade muda para \(V_{0} + {\Delta}V\) e a pressão na válvula torna-se \(p_{0} + {\Delta}p\), a densidade do fluido, \({\rho}_{0}\) , é alterada para \({\rho}_{0} + {\Delta}{\rho}\) , e a onda de pressão de magnitude  se desloca para montante, representado por \({\Delta}H\)na Figura 3.2. Destaca-se que a velocidade de propagação da onda é a celeridade \(a\).

Considerando \(0<{\Delta}t{\geq}\frac{L}{a}\) sendo \(L\) o comprimento da tubulação e \(a\) a celeridade, que é a velocidade de propagação da onda de pressão:

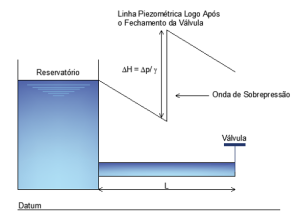
Figura 2 – Descrição do golpe de aríete, fechamento da válvula e compressão do líquido

À medida que a onda de sobrepressão se propaga pelo tubo com uma velocidade (celeridade) a, a massa de água que se encontra antes da onda de sobrepressão (\(m={\rho}Aa{\Delta}t\)) é instantaneamente paralisada (indo de uma velocidade \(V_{0}\) ao repouso). Aplicando a segunda lei de Newton a esta massa de água:

\({\Delta}pA = m\frac{{\Delta}V}{{\Delta}t} = -{\rho} Aa{\Delta}t\frac{{\Delta}V}{{\Delta}t} = -{\rho}Aa{\Delta}V\)

Assim, \({\Delta}{\rho}=-{\rho}a{\Delta}V\) é a sobrepressão causada pelo Golpe de Aríete. Sabendo que \({\Delta}H=\frac{{\Delta}p}{\gamma}\) temos:

\({\Delta}H=-\frac{a{\Delta}V}{g}\)

O sinal negativo do lado direito da equação acima indica que a pressão aumenta \({\Delta}H>0\) com a redução da velocidade e vice-versa. Diante disso, destaca-se que esta equação foi obtida para o caso em que a velocidade tem sentido de jusante, enquanto a onda de pressão tem sentido de montante, sendo, portanto, esta fórmula é conhecida como Fórmula de Allievi ou Fórmula de Allievi-Joukowsky. Ela é válida para um fechamento rápido de uma válvula (tempo de fechamento \(t{\leq}2\frac{L}{a}\) ).

É muito importante ressaltar que esta equação simples somente é válida para fechamento rápido de registros em tubos curtos.

 

3. Equações Fundamentais dos Transientes Hidráulicos

As duas equações que regem o fenômeno do Golpe de Ariete são a Equação de Conservação da Quantidade de Movimento ou do Momento:

\(\frac{{\theta}Q}{{\theta}t}+gA\frac{{\theta}H}{{\theta}x}+f\frac{Q|Q|}{2DA} = 0\)

 

E a Equação de Conservação da Massa ou Equação da Continuidade:

\(a^{2}\frac{{\theta}Q}{{\theta}x} + gA\frac{{\theta}H}{{\theta}t} = 0\)

 

onde

\(f \) – Fator de atrito de Darcy-Weisbach

\(D\) – Diâmetro do tubo – (\(L\))

\(H\) – Carga Hidráulica – (\(L\))

\(Q\)  – Vazão – (\(L^{3} T^{-1}\))

\(a\) – Celeridade – (\(LT^{-1}\))

\(g\) – Aceleração da gravidade – (\(LT^{-2}\))

A fim de solucionar as equações anteriormente apresentadas, cientistas vêm estudando há mais de um século, iniciando os estudos de transientes em fluidos, com a investigação das ondas sonoras no ar, propagação de ondas em águas rasas e fluxo de sangue nas artérias. Chaudhry (2014), Wylie et al. (1993) estudaram o golpe de aríete, aplicando-o computacionalmente, analisando modelos de redes de distribuição e mistura gás/líquido.

O Método Numérico mais utilizado atualmente para a solução das equações que regem os transientes hidráulicos em condutos forçados  é o método das características (MOC), consistindo em uma operação numérica de fácil iteratividade, que se baseia no conceito de derivada total no cálculo diferencial. As equações que governam o transiente hidráulico formam uma equação diferencial parcial linear de 2ª ordem Quasi-Hiperbólica. Através do método das diferenças finitas, essas equações são transformadas em homogêneas, ou seja, trabalha-se somente com uma variável independente.

Para simulação de problemas transientes como desligamento abrupto de bombas e fechamento de registros em tubos longos, um método número deve ser usado para a obtenção das sobrepressões e subpressões do Golpe de Ariete.